本文共 1419 字，大约阅读时间需要 4 分钟。

在逆向中我们无法使用breakpoint set -n "-[xxxxx xxxx:]"的方式（通过类名和方法名）来打断点，这种方式适合在Xcode工具中使用， 在逆向中我们一般使用breakpoint set -a 地址来打断点 ，通过函数的内存地址来打断点

那么我们如何找到正确的函数地址了？

1. Mach-O文件分析

首先我们知道Mach-O的文件结构：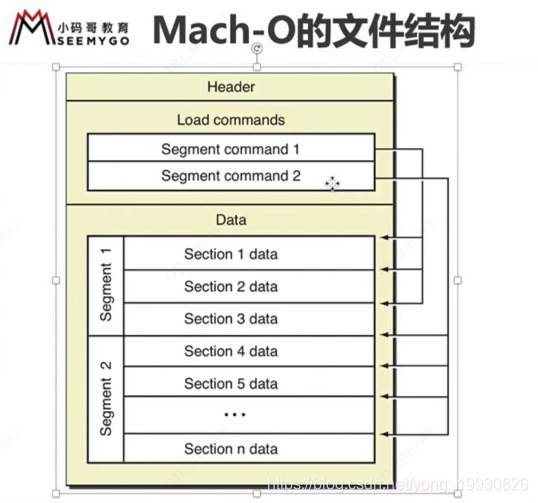

我们可以使用MachoView来分析下Mach-O文件的结构: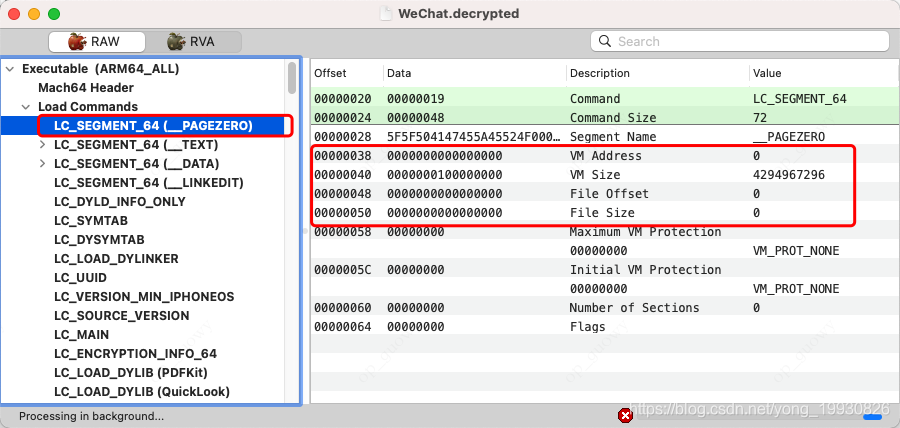

• VM Addreess: Virtural Memeory Address内存地址，在内存中的大小
• VM SIze:Virtural Memeory Address内存大小，占用内存多少
• _PAGEZERO、_TEXT、_DATA、_LINKENIF 的内存地址和内存大小都可以通过Mach-O文件
• File Offset:在Mach-O文件中的位置
• File Size: 在Mach-O文件中占据的大小

首先我们观察Mach-O文件，我们发现_PAGEZERO在Mach-O文件中是不存在的， 在内存中确是存在的

未使用ASLR的Mach-O文件加载到内存中的过程图：

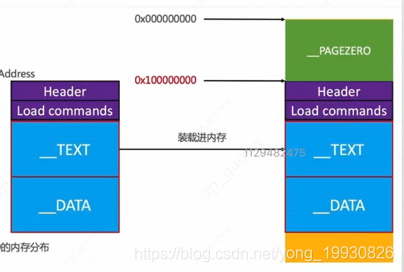
• 函数代码存放在_TEXT（_text）段中
• 全局变量存放在_DATA断中
• 可执行文件的内存地址是0x0
• 代码段（_TEXT）的内存地址
  • 就是LC_SEGMENT(_TEXT)中的VM Address
  • arm64: 0x100000000(8个0)
  • 非arm64：0x4000(3个0)
• 可以使用size -l -m -x来查看Mach-O的内存分布

2. ASLR

2.1 什么是ASLR

• Address Space Layout Randomization,地址空间布局随机化
• 是一种针对缓冲区溢出的安全保护技术，通过对堆、栈共享库映射等线性布局的随机化，通过增加攻击者预测目的地的难度，防止攻击者直接定位攻击代码位置，达到阻止溢出攻击目的的一种技术
• IOS4.3开始引入的ASLR技术

2.2 获取函数的真实地址

• 函数的内存地址（VM Address）= File Offset + ASLR Offset + _PAGEZERO
• Hopper、IDA中的地址都是未使用ASLR的VM Address
• 使用了ASLR技术的Mach-O加载进内存的过程：

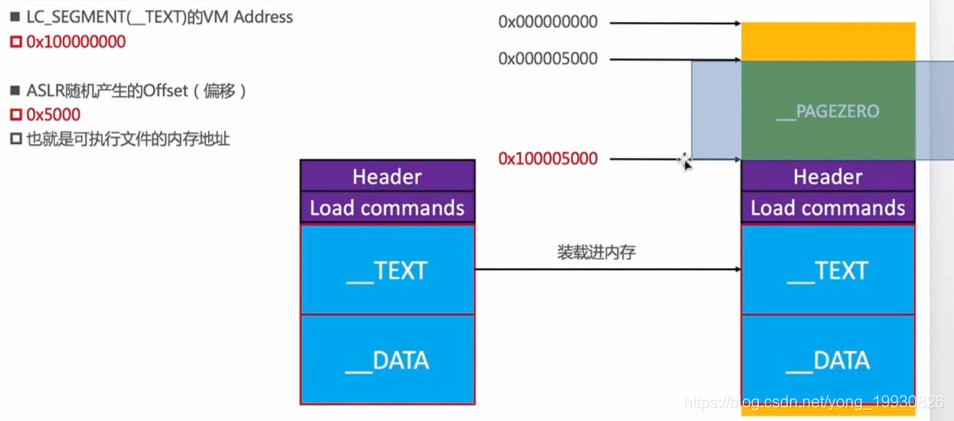
我们在程序中编写的函数，全局变量，程序一旦编译，函数和变量的位置就固定了，文件的偏移是固定的

我使用debugserver链接上手机查看微信Mach-O文件载进内存的地址，这样我们就可以获取函数真正的内存地址了，通过image list -o -f 查看模块信息，Mach-O文件本身也是一个模块：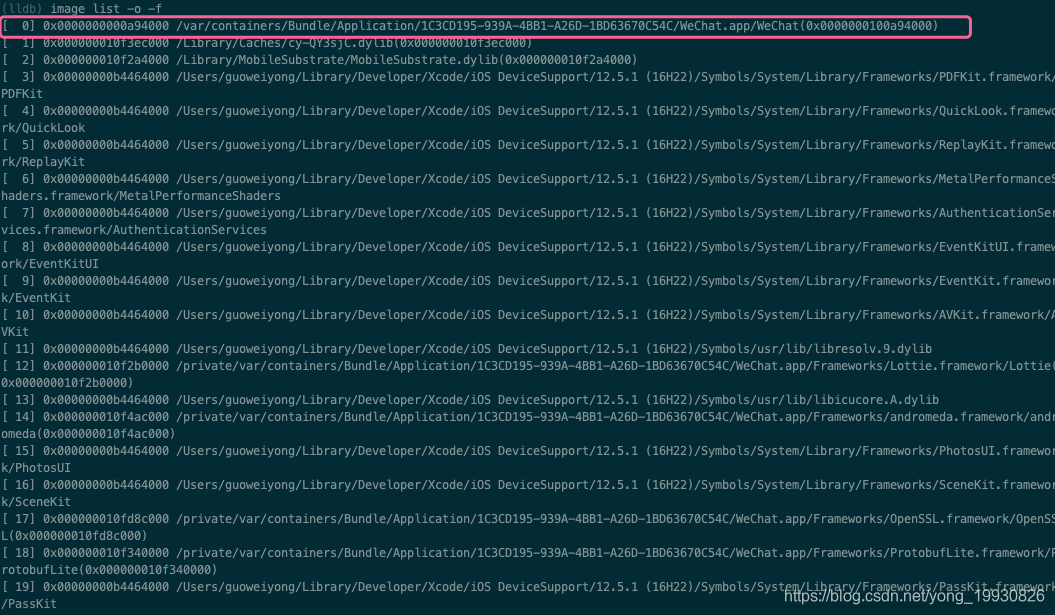

• 由上图可知，微信加载进内存的地址是什么，然后减去arm64架构固定长度（0x100000000），就得到ASLR技术造成的地址偏移量，然后我们在分析工具中看到的函数地址加上这个偏移量，就得到了函数在内存中真正的地址，这样我们就可以使用LLDB命令通过函数地址来打断点

虚拟内存的分配 ：dyld(动态库加载器) --> Mach-O文件(当前app的可执行文件) ---> 依赖的其他动态库（比如系统的UIKit等） ---> 栈空间、堆控件

3. 答疑

• _PAGEZERO的作用？
  • obj = NULL:NULL指针，其实就是指向_PAGEZERO安全区域

转载地址：http://xxrgz.baihongyu.com/